Web Ontology Language (OWL)

Recap

In our prior post we discuss description logics (DLs), a family of mathematical knowledge representation languages which are often used rather than first order logic (FOL)

To finish our suite of knowledge representation languages we discuss the Web Ontology Language, usually referred to as OWL.

OWL vs DL

OWL is another knowledge representation language, based on Description Logics. Unlike description logics and FOL, it is specified as a language which is contained in digital files rather than mathematical symbols.

Technically speaking, there exists OWL 1, the first version of OWL; OWL 1.1, an extension of OWL 1; and OWL 2 the second version of OWL. This paper outlines these changes. OWL 2 FULL refer to the whole of OWL 2 (without any restrictions).

The differences between OWL and Description Logics include:

• OWL 2 FULL is not decidable but most description logics are. Decidability is mentioned in our DL blog.
• The OWL 2 specification specifies "profiles"/"fragments", subsets of OWL which are decidable and closely correspond to a particular DL. These profiles are produced by removing some of the capability of OWL 2 FULL.

OWL 2 Profiles

OWL 2 DL is OWL 2 FULL with only the minimum restrictions placed on its capability to make it decidable. OWL 2 DL is based on the \(\mathcal{SROIQ}\) description logic.

OWL 2 specifies three profiles of OWL 2 DL which each have additional restrictions placed on them for greater reasoning efficiency. These restrictions are different for all three profiles, and it cannot be truly said that any of them are "more" logically expressive than another, just that they are differently expressive. They are :

• OWL 2 EL, based on \(\mathcal{EL++}\)
• OWL 2 QL, based on \(\mathcal{DL-Lite}\)
• OWL 2 RL, based on \(\mathcal{DLP}\)

The relationship between OWL 2, OWL 2 profiles, FOL and DLs are represented in Figure 1 below.

From FOL to OWL

Finally, let us provide some examples of how simple ideas could be represented in FOL, DL and OWL

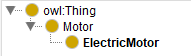
Example 1: Electric Motors are Motors

In First Order Logic, we can express this using the \(\forall\) quantifier, the \(\longrightarrow\) binary connective and the \(ElectricMotor\) and \(Motor\) unary predicates: \(\forall x (ElectricMotor(x) \longrightarrow Motor(x))\)

In Description Logic, we can express this using the \(ElectricMotor\) and \(Motor\) concepts and concept inclusion (\(\sqsubseteq\)) : \(ElectricMotor \sqsubseteq Motor\)

We can represent this concept in OWL through the text in Figure 2 below, which protege can visualise to produce Figure 3.

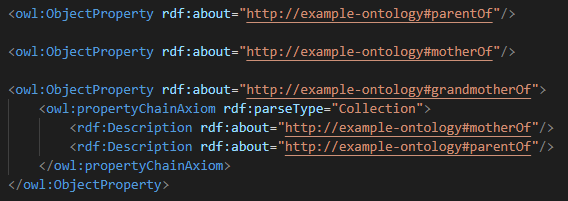
Example 2: The mother of the child's parent is a grandmother of the child

In First Order Logic, we can express this using the \(\exists\) and \(\forall\) quantifiers, the \(\longrightarrow\) binary connective and the \(motherOf\), \(parentOf\) and \(grandmotherOf\) binary predicates: \( \forall x, y (\exists z ( motherOf(x, z) \land parentOf(z, y)) \longrightarrow grandmotherOf(x, y))\)

In DL, we can express this using role composition (\(\circ\)), role inclusion (\(\sqsubseteq\)) and the \(motherOf\), \(parentOf\) and \(grandmotherOf\) roles. \( motherOf \circ parentOf \sqsubseteq grandmotherOf\)

We can represent this concept in OWL through the text in Figure 4 below, which protege can visualise to produce Figure 5.

Conclusion

We hope that this blog series has served as a useful introduction to knowledge representation for engineers and others collaborating with ontologists. We have only presented the most simple examples of the potential application of these powerful tools.

For any questions or comments please contact Marcus Handley, marcus.w.handley@gmail.com or Caitlin Woods, caitlin.woods@research.uwa.edu.au. Written by Marcus Handley, edited by Caitlin Woods, Emily Low, Frinze Lapuz and Melinda Hodkiewicz.